Le rapport a / b est  égal au nombre d'or lorsque a est à b ce que a + b est à a. Le rapport de a sur b est égal au rapport de a + b sur a :
 Le rapport de la somme des deux longueurs (a+b) sur la plus grande (a) est égal à celui de la plus grande (a) sur la plus petite (b) :

Le nombre d'or est l'unique solution positive de l'équation x² = x + 1. Il vaut exactement :

 

Rectangle d'or

...

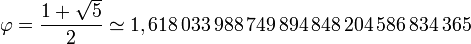
Un rectangle est dit d'or si le rapport entre la longueur et la largeur est égal au nombre d'or.

Pour tracer un rectangle d'or de longueur a et de largeur b, le plus simple est de dessiner un carré de côté b. En prenant le milieu de la base comme centre, on trace un cercle passant par les deux sommets opposés. L'intersection de la droite prolongeant la base du carré et du cercle détermine l'extrémité de la base du rectangle d'or. Il apparait comme construit par l'adjonction à un carré de côté de longueur b, d'un rectangle de côtés de longueur b et a - b, comme le montre la figure de droite.